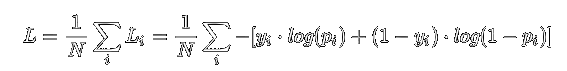全连接神经网络识别MNIST手写数字集,AI中的HelloWorld
全连接神经网络[神经网络入门]
前言
现在的AI库诸如TensorFlow,Keras,Pytorch等,都可以快捷方便地在几行代码之内就构建好一个网络模型,然后开始训练等后续的事情,但把这些库当成黑盒来用的话,反正我是晚上睡不着觉的
虽然说全连接神经网络(Fully Connected Neural Network,以下简称FCNN)是人造神经网络(Artificial Neural Network,以下简称ANN)的入门,但在这之前也可以先做一些线性回归,逻辑回归,以及逻辑回归的多分类来加深理解和降低入门的难度,这些也是我之前做过的东西,但因为写的比较烂而且本身也不难,就不放出来了
因为在这篇文章之前只有这篇讲对抗扰动的文章 是有关机器学习的,所以我也尽量在这篇文章中细🔒一些概念和理解,最好能让吃瓜的也能吃的舒服
ANN概述
对于神经网络的认识和理解,强烈推荐3b1b的系列视频 (共四集),从概念到公式一条龙服务,讲的肯定比我清楚和直观
对于系统学习机器学习的相关知识(包括线性回归,逻辑回归等),可以看吴恩达系列视频 (这个就有点多了)
ANN是什么
神经网络不是玄学,全是数学,具体点,我目前做的东西涉及到的概念其实也就:偏导数,线性代数,链式法则,都是大一就学过的东西
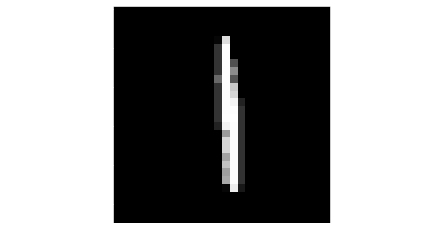
本文会讲解如何训练一个识别MNIST手写数字集的神经网络,MNIST手写数字集是包含了数万张28x28的手写数字图像的数据集(以下简称MNIST,但其实还有MNIST衣物图片的数据集等),每个数字对应了一个lable,指明图像对应的数字,如下图就是一份数据集中包含的数据样本,而他对应的lable是1
抽象的说,神经网络就是一个函数(这样思考对于CTF中构造对抗样本很有帮助),你给他一个输入,他给你一个输出
记这个网络为h(hypothesis),这个输入的1的数字图片样本记为X,则我们所期待的是模型输出一个向量来描述各个数字的概率h(X)={0,1,0,0,0,0,0,0,0,0}(从左到右是0至9的概率,意思模型认为图片是1的概率是100%,是除了1以外的数字的概率是0%,这样的格式称为OneHot Encoding,好处是便于矩阵计算)
ANN为何表现出智能
在3b1b的视频中,他在Part1的5:40提到
Why it's even reasonable to expect a layered structure like this to behave intelligently
他给出了一个比较让人容易接受的理解,即在多层次的结构中,上一层处理出图像的一些细微特征,然后在下一层对这些特征进行组合
但显然真正的网络并不是这样工作的,在3b1b的视频中,他在Part2的14:25展示了一些神经网络的权重可视化,而直观上看可视化后的权重,基本就是稍微有序一些的噪音,所以关于这个网络怎么能够得到我们所期待的功能那是这个网络自己的事情(“你已经是一个成熟的神经网络了”),只要他找到了一个还算不错的局部最优解,那其实就已经足够了
总结一下就是,把ANN看成一个数学模型就行,千万别想玄乎了,在生物上的神经科学发展完全之前,对“智能”的定义都会是比较模糊的,我们就算感觉AI好像拥有智能,那也只不过是一个结构比较复杂的函数
一个神经元
我很喜欢的一句话:简单的规则可以组成复杂的系统,这句话在神经网络中同样适用,先理解单个神经元的工作原理,才能理解他们组成的网络是如何工作的,在后续对神经网络的数学推导中,我也会先对单个神经元组成的网络推导,然后再推广开来,方便我这样🧠不太好的人理解(这也是3b1b的做法,太照顾人了
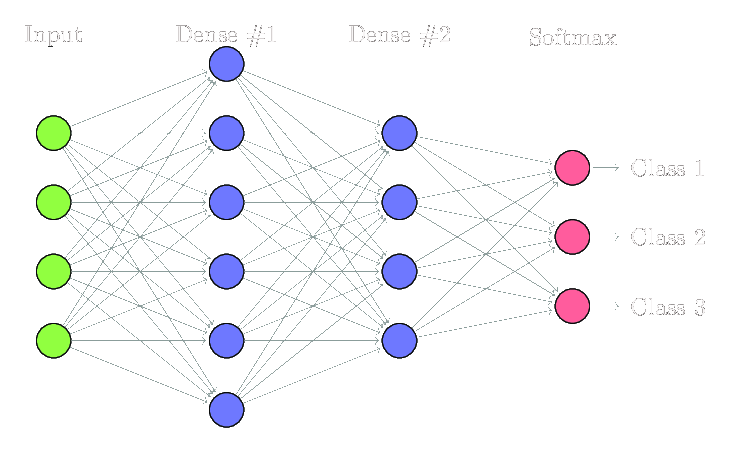
以下内容均以下图所示网络为例
首先明确,FCNN是一个多层次结构,包含了输入层,隐藏层,输出层
单个神经元的机理很简单,观察隐藏层Dense #2中的第0个神经元,它也是一个函数,记作Z[2][0],其中,Z表示神经元函数本身,[2]表示其在第二层,[0]表示其是第一个神经元,由图可知,它的输入是其上一层的所有神经元的输出,它的输出会传递到下一层的每一个神经元,这也是“全连接”的直接体现(你要是看到图里面他没有全连接起来,那多半是我抠图的时候魔棒不小心扣没了)
而神经元之间的信号传递其实是一个线性的过程,类比y=kx+b,即
Z[2][0]=∑w[2][i][0]*Z[1][i] for i in range(0,6)
WARNING: 这个式子是错的,但暂时先这样理解
在w[2][i][0]中,w表示权重(类比k,具体点,可以把w相成是神经元之间连接的线),[2]表示该权重是第一层与第二层之间的,[i]表示上一层中的第i个,[0]表示下一层中的第0个(表达上有点繁琐,但并不难理解)
偏置
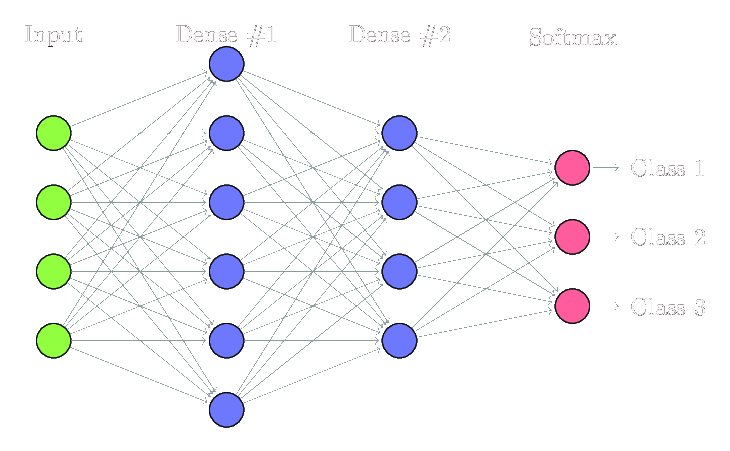
显然相对于y=kx+b,还少了其中的b,为了补上b,在FCNN中,会给除了输出层之外的每一层补上一个神经元作为bias,又称偏置,这是一个特殊的神经元,其不接受任何输入,然后对下一层中的每一个神经元都稳定输出一个+1,然后下一层中偏置对每个神经元影响的大小再由对应的权重来调整,具体的连接方式如图白色部分所示
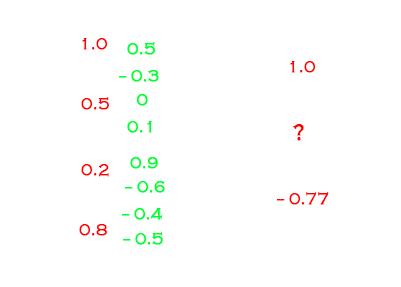
现在可以试着举一个例子了,比如考虑如下情况?的值
而问号的下面那个神经元的值,是-0.3+0.05+(-0.12)+(-0.4)=-0.77
激活函数
如果直接把线性计算得到的Z作为该神经元的输出传递到下一层,那么得到的网络也将是一个线性网络,这样的网络不管是十层还是百层都只能相当于一层
为了得到一个非线性的网络,在除了输入层之外的每一层都会在Z的基础上再套一个激活函数A,激活函数以Z作为输入,即神经元的输出其实是A(Z)
常见的激活函数有:ReLU,tanh,sigmoid等,就不附图了搜一下就有(懒
那么,更新一以下之前提到的Z的式子,应该是
Z[2][0]=∑w[2][i][0]*A[2][i], i for i in range(0,6)
(由于偏置作为一个神经元包含进上一层的输出,就不在式子中单独加上一个b了)
对于输出层,激活函数则要根据具体问题来选择,例如MNIST手写数字集是分类0至9的数字,有多个类别,则会选用softMax作为输出的激活函数,其特征是累加之和为1,这符合多分类的问题的期望解,更具体的东西,比如softMax的求偏导,具体公式之类的,就不赘述了(懒
流程梳理
以下梳理一下数据传递的整体流程
输入的数据为X(输入层),直接输入到隐藏层
隐藏层第一层的输出为A1(Z1),其中Z1=w1*X
隐藏层第二层的输出为A2(Z2),其中Z2=w2*A1
......以此类推
训练过程
主要就是梯度下降,一句话,求梯度,然后往负梯度的方向行进,可以求得一个函数的极小值,但是:为什么梯度下降这个方法可以训练一个模型,具体是怎么implement的,大概就到了大多数人的认知边界了/滑稽。考虑梯度下降之前,先了解求梯度的应用对象:损失函数
损失函数
loss/cost function,记作J,是描述模型的预测结果对于真实值的差异的函数,举个例子,给了模型1的图片输入,模型的输出却是{0.5,0.5,0,0,0,0,0,0,0,0},这与应该出现的结果产生了偏差,要描述这个偏差,可以直接求实际输出向量和期望的输出向量之差的L2范数,即求他们的均方误差,记期望的向量为y,实际输出的向量为h(x),则J=∑((y-h(x))*(y-h(x))),此处乘积为对应元素相乘,则计算可得loss大约是0.71
通过损失函数,就可以量化表示模型预测结果的准确度了,而大多数时候会使用较复杂度更高的带log的交叉熵函数作为损失函数,公式如下
看起来比较复杂,但画一个抛物线来表示均方误差函数,再画一下log的图像理解交叉熵函数就差不多了
交叉熵好处都有啥:收敛快,局部最优点少,知道就行
梯度下降
除了单纯的梯度下降,还有如momentum,RmsProp,Adam等优化算法,但本文使用mini-batch梯度下降法来训练
首先明确常量:训练时用的样本X是固定不变的,样本对应的lable,或记作y,也是不变的,唯一变化的就只有网络中间连接各个层级的权重w(偏置b包含在权重里边,因为偏置的具体大小由连接的权重控制),以及因为权重变化而跟着一起变化的预测结果,还有中间量A和Z,一切变化都来自于权重w的变化
问题现在则应该理解成:找到合适的w,使得J最小
具体点,就是:对J(w)求关于w的偏导,获取J(w)的梯度,然后更新权重w为w-=rate*dw,其中,dw为J(w)的梯度,rate为学习率,控制了一次下降多少,学习率过低会导致训练缓慢,学习率过高则容易各种NAN或者反复横跳无法收敛,需要一定的试错成本来确定合适的学习率,一般在10e-6到1之间
由于这部分内容网上资源挺多的,就不赘述了(懒
(后面会有反向传播的推导,这才是重点
具体实现
以上就是一些重要的前置(因为我怕把理解和代码融为一体会导致逻辑混乱),以下内容就正式开始涉及码代码了,坐好扶稳
预处理
在kaggle下载到他们提供的MNIST手写数字数据集后,不能上手即用
颜色范围0至255这个区间太大了,应该压缩到0至1,整体除以255
再者数据的分布也不自然,应该套一个标准分数公式,处理成正态分布
关于应该对单个像素做处理还是对整体做处理(例如求均值,是对每一个像素求出对应像素位置的均值,还是整体处理,直接求出所有像素的均值),在本例中应该整体处理更好
Source
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 dsTrain = pd.read_csv(r'mnist.csv' ) dsTest = pd.read_csv(r'mnist_test.csv' ) ''' # 获取训练集的特征 ds_std = np.std(dsTrain.iloc[:, 1:], axis = 0) # 训练集标准差 ds_mean = np.mean(dsTrain.iloc[:, 1:], axis = 0) # 训练集均值 # 标准化数据,此方法是针对训练集中的同一位置的像素,效果一般,故未采用 for i in range(len(ds.T) - 1): if ds_std[i] != 0: # 边角上就很可能出现标准差为0的像素 dsR.iloc[:, i + 1] = (dsR.iloc[:, i + 1] - ds_mean[i]) / ds_std[i] # 标准分数公式,基本呈正态分布 ''' trainX = dsTrain.iloc[:, 1 :] trainy = dsTrain.iloc[:, :1 ] testX = pd.concat([dsTest[dsTest["label" ] == i].iloc[:, 1 :] for i in range (10 )]) testy = pd.concat([dsTest[dsTest["label" ] == i].iloc[:, :1 ] for i in range (10 )]) trainX = trainX / 255 testX = testX / 255 mean = np.mean(np.array(trainX).ravel()) std = np.std(np.array(trainX).ravel()) trainX = (trainX - mean) / std testX = (testX - mean) / std
数学函数
之前提到了一堆数学函数,实现起来主要就是softMax和sigmoid会比较耽误时间
leaky ReLU是ReLU的实验性变种,通常用于在实验的时候避免因为使用ReLU导致大量神经元死亡,梯度消失的问题
后记:之前的SoftMax偏导求错了,其应该是一个方阵,但估计是因为一开始写的时候为了方便,没有理解清楚就去找了一段标称是derivative of softmax的代码,结果他求的只是在i=j情况下的的softmaxtensorflow中gradientTape求得的梯度比较时怀疑人生
Source
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 def relu (x ): return np.maximum(x, 0 ) def d_relu (x ): return x > 0 def lrelu (x ): return np.maximum(x, 0.1 * x) def d_lrelu (x ): return (x > 0 ) * 0.9 + 0.1 def softMax (x ): return np.array(np.exp(x) / np.sum (np.exp(x), axis=1 )) def d_softMax (x ): x = softMax(x) r = [] for i in range (x.shape[0 ]): for j in range (x.shape[1 ]): r.append([]) for k in range (x.shape[1 ]): r[-1 ].append(-x[i][j] * x[i][k] if j != k else x[i][j] * (1 - x[i][k])) return np.array(r) def sigmoid (x ): x_ravel = np.array(x).ravel() length = len (x_ravel) y = [] for i in range (length): if x_ravel[i] >= 0 : x_ravel[i] = min (19 , x_ravel[i]) y.append(1.0 / (1 + np.exp(-x_ravel[i]))) else : x_ravel[i] = max (-744 , x_ravel[i]) y.append(np.exp(x_ravel[i]) / (np.exp(x_ravel[i]) + 1 )) return np.array(y).reshape(x.shape) def d_sigmoid (x ): return sigmoid(x) * (1 - sigmoid(x))
数据处理函数
之前提到的OneHot和插入bias
Source
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 def OneHot (length, width, y ): y = np.array(y).ravel() r = np.zeros((length, width)) for i in range (length): r[i][int (y[i])] = 1.0 return r def AddBias (x ): x = np.matrix(x) return np.c_[np.ones((x.shape[0 ], 1 )), x] def RemoveBias (x ): return np.matrix(x)[:, 1 :]
FCNN class
以下开始填充FCNN类
明确一下类中的基本函数
1 2 3 4 5 6 7 8 9 class FCNN : def Init (self, unitNum ) def PrepareBatch (self, X, y, batchSize=0 ) def fit (self, epoch, rate ) def gradDes (self, rate ) def backProp (self ) def forwardProp (self ) def ClrTempResult (self ) def predict (self, X, y )
明确一些概念
batchSize:如果整个过完一遍训练集中的数据才更新一次权重,则更新速度过慢,故将数据集拆分为多批来处理,batchSize就是一批数据有多少份样本
epoch:总共要过几遍完整的数据,所以权重的更新次数就是epoch*N/batchSize,其中N是训练集样本总量
backward Propagation:后向传播,指通过梯度来调整权重的过程(重点)
forward Propagation:前向传播,指传入样本后得到输出结果的过程
以上概念虽然名词是在本文中第一次出现,但结合上文都不难理解
而训练过程中还有一个称作DropOut的优化方法,指的是在训练中随机地掐死一些神经元,前向传播的时候不经过他们,后向传播的时候也不更新他们,从而使得模型更具鲁棒性,也可以有效避免模型过拟合(过拟合:模型泛化不好,训练集和测试集的识别准确率相差过大),关于DropOut为什么能增强模型鲁棒性、避免过拟合的说法有很多,建议自己搜(懒
然后我们肯定希望模型可以保存下来,至少训练出来的权重得能保存吧,不然每次都得重来一遍
所以再补几个函数
1 2 3 4 class FCNN : def GetDropOut (self ) def SaveParameters (self ) def LoadParameters (self )
其中backProp的公式推导这个重点问题放到下面的模块来说,这里则再提一些小一点的问题
权重的初始化方法
选择错误的权重初始化方法会导致梯度消失等严重问题,可能导致训练根本无法开始,由于我选择的是ReLU作为隐藏层的激活函数,使用了He initialization,具体为什么这样的初始化对ReLU会更友好则没有深入探究
正则项
有一种防止过拟合的方法是:在损失函数中加入有关权重w的二次项,这样在dw中就体现在每次更新权重时权重都会自减一点点
DropOut的具体实现
创建与w同样size的矩阵,将本轮中掐死的神经元的行与列置0,其他置1,传递时把w换成np.multiply(w,dropOut)即可
Source
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 class FCNN : def Init (self, unitNum, dropOutProb=[] ): ''' 完成一些初始化 unitNum: list 每一层的神经元数量 dropOutProb: list 除了输出层以外每一层的dropOut概率(0,1) ''' self.unitNum = unitNum self.layerNum = len (unitNum) self.dropOutProb = dropOutProb if dropOutProb else [0 for i in range (self.layerNum - 1 )] self.outLength = unitNum[-1 ] self.w = [0 ] self.Z = [0 ] self.A = [0 ] self.cost = [] self.costTemp = [] self.dwNorm = [] self.dwNormTemp = [] for i in range (1 , self.layerNum - 1 ): np.random.seed(i) self.w.append(np.matrix(np.random.randn(unitNum[i - 1 ] + 1 , unitNum[i])) * np.sqrt(2 / unitNum[i])) self.w[-1 ][0 ] = np.matrix(np.zeros((1 , unitNum[i]))) np.random.seed(self.layerNum - 1 ) self.w.append(np.matrix(np.random.rand(unitNum[-2 ] + 1 , unitNum[-1 ]))) self.w[-1 ] = (self.w[-1 ] - np.mean(self.w[-1 ])) / np.std(self.w[-1 ]) / 100 self.w[-1 ][0 ] = np.matrix(np.zeros((1 , unitNum[-1 ]))) self.ClrTempResult() def PrepareBatch (self, X, y, batchSize=0 ): ''' 分割训练集并完成一些初始化 batchSize: 每一批样本的数量,需能被样本总数整除 ''' N = X.shape[0 ] if not batchSize: batchSize = N if N % batchSize: print("# ERR: illegal batchSize" ) return self.batchSize = batchSize self.batchTime = int (N / batchSize) self.X = np.matrix(X) self.y = OneHot(X.shape[0 ], unitNum[-1 ], y) self.batchX = [] self.batchy = [] self.batchTime = int (N / batchSize) for i in range (self.batchTime): self.batchX.append(np.array(self.X[i * batchSize : (i + 1 ) * batchSize])) self.batchy.append(self.y[i * batchSize : (i + 1 ) * batchSize]) print("\rPreparing: %.2f%%" % ((i + 1 ) / N * batchSize * 100 ), end="" ) def fit (self, epoch, rate ): ''' epoch: int 训练轮次 rate: float 学习率 ''' N = self.X.shape[0 ] for i in range (epoch): for j in range (self.batchTime): self.Z[0 ] = self.batchX[j] self.A[0 ] = self.batchX[j] self.y = self.batchy[j] self.gradDes(rate) self.ClrTempResult() print( "\rTotalProgress: %.2f%% BatchProgress: %.2f%% " % (((i + 1 ) / epoch * 100 ), ((j + 1 ) / N * self.batchSize * 100 )), end="" , ) self.cost.append(sum (self.costTemp) / self.batchTime) self.costTemp.clear() self.dwNorm.append(np.sum (self.dwNormTemp, axis=0 ) / self.batchTime) self.dwNormTemp.clear() def gradDes (self, rate ): self.backProp() ''' # 一种较为简单的损失函数 J(θ) J = np.sum(np.multiply(self.y-self.A[-1],self.y-self.A[-1]))/self.batchSize # 这里使用更加复杂的带有log的交叉熵函数 ''' J = (-np.sum (np.array(self.y) * np.log(self.A[-1 ]) + np.array(1 - self.y) * np.log(1 - self.A[-1 ])) / self.batchSize) self.costTemp.append(J) dwNt = [] for i in range (1 , len (self.w)): dwNt.append(np.linalg.norm(self.dw[i])) self.w[i] -= rate * self.dw[i] self.dwNormTemp.append(dwNt) def GetDropOut (self ): index = [] prob = self.dropOutProb[0 ] num = 0 if not prob else int (np.clip(np.random.randn() / 50 + prob, 0 , 0.75 ) * self.unitNum[0 ]) index.append(np.random.choice(self.unitNum[0 ], num, False )) for i in range (1 , self.layerNum - 1 ): prob = self.dropOutProb[i] num = 0 if not prob else int (np.clip(np.random.randn() / 50 + prob, 0 , 0.75 ) * self.unitNum[i]) index.append(np.random.choice(self.unitNum[i], num, False )) dropOutMat = np.ones((self.unitNum[i - 1 ], self.unitNum[i])) for j in index[i - 1 ]: dropOutMat[j] = np.zeros((1 , self.unitNum[i])) dropOutMat = np.transpose(dropOutMat) for j in index[i]: dropOutMat[j] = np.zeros((1 , self.unitNum[i - 1 ])) dropOutMat = np.r_[np.ones((1 , self.unitNum[i])), np.transpose(dropOutMat)] self.dropOut.append(np.matrix(dropOutMat)) dropOutMat = np.ones((self.unitNum[-2 ], self.unitNum[-1 ])) for j in index[-1 ]: dropOutMat[j] = np.zeros((1 , self.unitNum[-1 ])) dropOutMat = np.r_[np.ones((1 , self.unitNum[-1 ])), dropOutMat] self.dropOut.append(np.matrix(dropOutMat)) def backProp (self, d_lossFunc, forward=True , dX=False ): if forward: self.forwardProp() self.dA[-1 ] = d_lossFunc() self.dZ[-1 ] = [] Zt = np.array(self.Z[-1 ]) dAt = np.array(self.dA[-1 ]) for i in range (self.batchSize): self.dZ[-1 ].append(np.array(d_softMax(np.matrix(Zt[i])) * np.matrix(dAt[i]).reshape((self.unitNum[-1 ], 1 ))).ravel()) self.dZ[-1 ] = np.matrix(self.dZ[-1 ]) dw = self.A[-2 ].T * self.dZ[-1 ] db = np.sum (self.dZ[-1 ], axis=0 ) self.dw[-1 ] = np.r_[db, dw] / self.batchSize for i in reversed (range (1 , self.layerNum - 1 )): self.dA[i] = RemoveBias(self.dZ[i + 1 ] * np.multiply(self.w[i + 1 ], self.dropOut[i]).T) self.dZ[i] = np.multiply(d_relu(self.Z[i]), self.dA[i]) dw = self.A[i - 1 ].T * self.dZ[i] db = np.sum (self.dZ[i], axis=0 ) self.dw[i] = np.multiply(np.r_[db, dw] / self.batchSize, self.dropOut[i - 1 ]) if dX: self.dA[0 ] = RemoveBias(self.dZ[1 ] * np.multiply(self.w[1 ], self.dropOut[0 ]).T) self.dZ[0 ] = self.dA[0 ] def forwardProp (self ): self.GetDropOut() for i in range (1 , self.layerNum - 1 ): self.Z.append(AddBias(self.A[-1 ]) * np.multiply(self.w[i], self.dropOut[i - 1 ])) self.A.append(relu(self.Z[-1 ])) self.Z.append(AddBias(self.A[-1 ]) * np.multiply(self.w[-1 ], self.dropOut[-1 ])) self.A.append(softMax(self.Z[-1 ])) def ClrTempResult (self ): self.Z = self.Z[0 :1 ] self.A = self.A[0 :1 ] self.dw = list (np.repeat(1 , self.layerNum, axis=0 )) self.dZ = list (np.repeat(1 , self.layerNum, axis=0 )) self.dA = list (np.repeat(1 , self.layerNum, axis=0 )) self.dropOut = [] def predict (self, X, y ): self.ClrTempResult() self.dropOutProb = [0 for i in range (self.layerNum - 1 )] self.Z[0 ] = np.matrix(X) self.A[0 ] = np.matrix(X) self.forwardProp() r_p = self.A[-1 ] self.r = np.zeros((r_p.shape[0 ], 1 )) correct = 0 self.wrong = [] for i in range (r_p.shape[0 ]): self.r[i] = np.argmax(r_p[i]) if self.r[i] == np.array(y).ravel()[i]: correct += 1 else : self.wrong.append(i) print("correct: " + str (correct / r_p.shape[0 ])) def SaveParameters (self ): f = open ("FCNNweight.dat" , "wb" ) wt = [] for i in self.w[1 :]: wt.extend(list (np.array(i).ravel())) f.write(np.array(wt).tobytes()) f.close() def LoadParameters (self ): f = open ("FCNNweight.dat" , "rb" ) wt = np.frombuffer(f.read(), np.float64) f.close() for i in range (1 , len (self.unitNum)): self.w[i] = np.matrix(wt[: (self.unitNum[i - 1 ] + 1 ) * self.unitNum[i]]).reshape((self.unitNum[i - 1 ] + 1 , self.unitNum[i])) wt = wt[(self.unitNum[i - 1 ] + 1 ) * self.unitNum[i] :]
后向传播推导
以下为我梳理代码的时候顺便写的过程
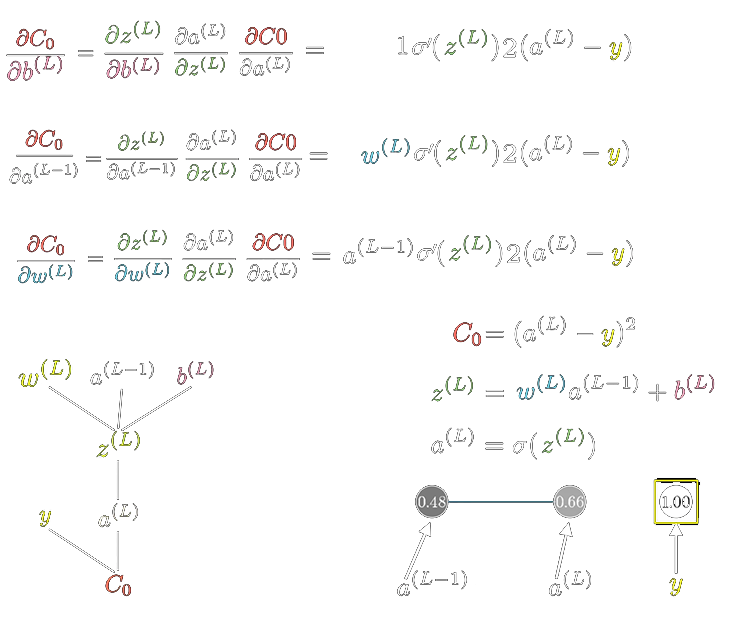
链式法则推单个神经元,然后扩展到矩阵
强烈建议搭配3b1b系列part4(或者是part3[下]?)食用,附上一张3b1b视频的截图
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 layerNum = 4 ''' input -> hidden 1 -> hidden 2 -> output 784+1 -> H1+1 -> H2+1 -> 10 Z0(X) ┌───>Z1 ┌───>Z2 ┌──>Z3 │ │ ↓ │ ↓ │ ↓ │ [w1] [relu] [w2] [relu] [w3][softmax] ↓ │ ↓ │ ↓ │ ↓ A0(X)──┘ A1─────┘ A2─────┘ A3 ''' unityNum = [784 , H1, H2, 10 ] w = [ 0 , [w1(784 +1 ,H1)], [w2(H1+1 ,H2)], [w3(H2+1 ,10 )] ] Z = [ [X(N,784 )] ] Z = [ [X(N,784 )], [Z1(N,H1)], [Z2(N,H2)], [Z3(N,10 )] ] ''' # u[i] indicates i.th layer of neural network # and each layer has only 1 neuron # L.th layer indicates output layer .... {u[L-1]}────{u[L]} # Deduction (lossFunc: CrossEntropy): - layer L : dA[L] = δJ/δA[L] = A[L] - y dZ[L] = δA[L]/δZ[L] * dA[L] = sigmoidDeriv(Z[L]) * dA[L] dw[L] = δw[L]/δZ[L] * dZ[L] = A[L-1] * dZ[L] db[L] = δb[L]/δZ[L] * dZ[L] = dZ[L] - layer L-1 : dA[L-1] = δZ[L]/δA[L-1] * dZ[L] = w[L] * dZ[L] dZ[L-1] = δA[L-1]/δZ[L-1] * dA[L-1] = reluDeriv(Z[L-1]) * dA[L-1] ... etc. ''' ''' # when each layer has more than 1 neuron {u[L-1][0]} ┌─{u[L][0]} .... {u[L-1][1]}══╡ └─{u[L][1]} {u[L-1][2]} # for a certain neuron in hidden layer, e.g. as for u[L-1][1] # w[L][1][0] indicates weight between {u[L-1][1]} and {u[L][0]} # Deduction : - layer L : dA[L][0] = A[L][0] - y[0] dA[L][1] = A[L][1] - y[1] dZ[L][0] = sigmoidDeriv(Z[L][0]) * dA[L][0] dZ[L][1] = sigmoidDeriv(Z[L][1]) * dA[L][1] dw[L][1][0] = A[L-1][1] * dZ[L][0] dw[L][1][1] = A[L-1][1] * dZ[L][1] db[L][1][0] = dZ[L][0] db[L][1][1] = dZ[L][1] - layer L-1 : dA[L-1][1] = w[L][1][0] * dZ[L][0] + w[L][1][1] * dZ[L][1] dZ[L-1][1] = reluDeriv(Z[L-1][1]) * dA[L-1][1] ... etc # e.g. as for 3.rd layer, which has index of 2 : dA2(N,H2) = RemoveBias(dZ3(N,10) * w3.T(10,H2+1)) dZ2(N,H2) = np.multiply(reluDeriv(Z2)(N,H2),dA2(N,H2)) dw2(H1,H2) = A1.T(H1,N) * dZ2(N,H2) db2(1,H2) = np.sum(dZ2(N,H2),axis=0) ''' dA = [ 1 , [dA1(N,H1)], [dA2(N,H2)], [dA3(N,10 )] ] dw = [ 1 , [dw0(784 +1 ,H1)], [dw1(H1+1 ,H2)], [dw2(H2+1 ,10 )] ]
main
1 2 3 4 5 6 7 8 9 10 11 unitNum = [784 , 512 , 256 , 10 ] dropOutProb = [0.4 , 0.2 , 0.1 ] batchSize = 120 epoch = 50 rate = 0.08 FCNN = FCNN() FCNN.Init(unitNum, dropOutProb) FCNN.PrepareBatch(trainX, trainy, batchSize) FCNN.fit(epoch, rate) FCNN.SaveParameters()
后续验证
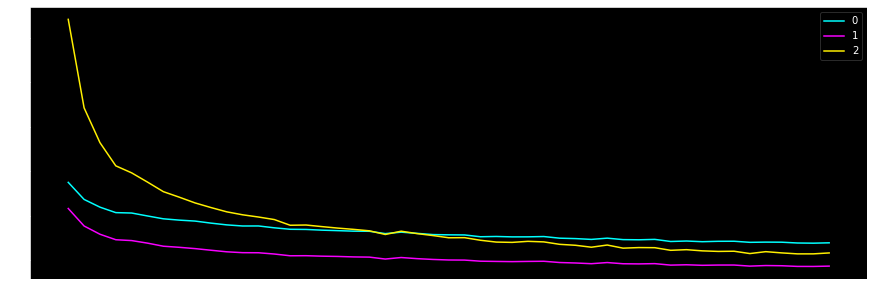
在训练完只会应当绘制loss图像,用于确保梯度下降是没有问题的(dw模长单纯是我想看一下而已)
Source
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 def ShowCostFig (epoch, cost ): ax = plt.figure().gca() ax.xaxis.set_major_locator(MaxNLocator(integer=True )) plt.plot(range (0 , epoch), cost[0 :], "go-" ) plt.show() print("Final Cost: " + str (cost[epoch - 1 ])) def ShowdwFig (epoch, dw, layerNum ): camp = getCmap(layerNum) ax = plt.figure(figsize=(15 , 5 )).gca() ax.xaxis.set_major_locator(MaxNLocator(integer=True )) for i, data in enumerate (np.transpose(dw)): plt.plot(data[1 :], c=camp(i), label=i) plt.legend() plt.show() def getCmap (n, name="hsv" ): """Returns a function that maps each index in 0, 1, ..., n-1 to a distinct RGB color; the keyword argument name must be a standard mpl colormap name.""" return plt.cm.get_cmap(name, n) def ShowNorm (x ): print("Norm: " + str (np.linalg.norm(x)))
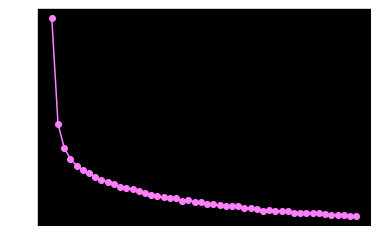
1 2 3 4 5 6 7 8 9 FCNN.predict(trainX, trainy) >> correct: 0.9768571428571429 FCNN.predict(testX, testy) >> correct: 0.9675 ShowNorm(FCNN.w[-1 ]) >> Norm: 4.553835257428929 ShowCostFig(epoch, FCNN.cost) >> Final Cost: 0.2906157343621473 ShowdwFig(epoch, FCNN.dwNorm, FCNN.layerNum)
可见loss的确在以肉眼可见速度收敛,且模型对训练集和测试集的预测准确度相差不大,都保持在96%~97%,对我来说我已经满意了
最后当然是喜闻乐见的错误样本抽样(只能说相当一部分的错误样本也都不是什么善茬